Thesis
Download
The thesis can be downloaded here (48 MB). A compressed version here (8 MB)
Summary
Clinical/industrial applications
I did my PhD in mathematical/medical image analysis with the thesis "Retinal Image Analysis using Sub-Riemannian Geometry in SE(2)". The thesis describes algorithms for the automatic and semi-automatic analysis of retinal images. These retinal images are obtained via non-invasive optical cameras that image the inside of the eye. The goal for developing automated retinal image analysis algorithms was twofold:
- To facilitate large scale clinical studies aimed at discovering new biomarkers and monitoring disease progression through observations in the eye.
- To facilitate computer assisted diagnosis/referral systems.
Brain-inspired mathematics
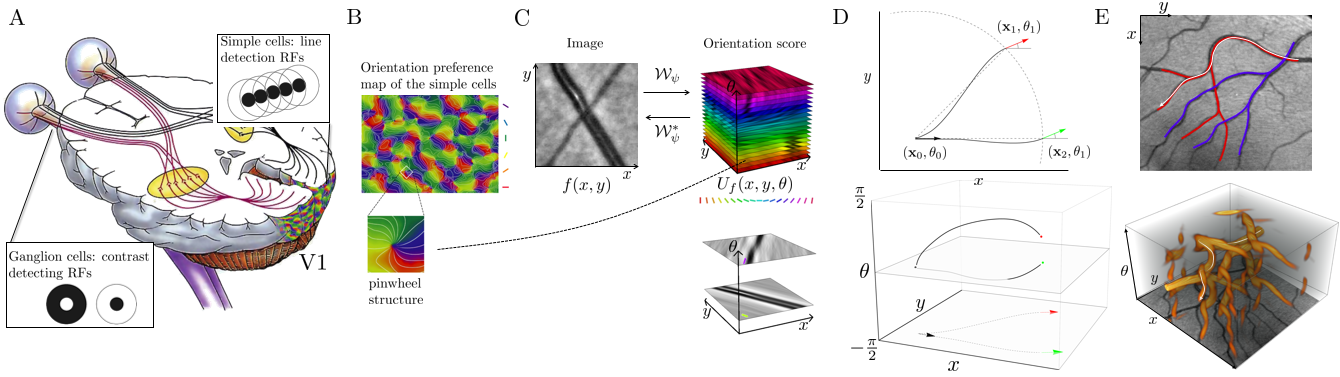
In my thesis I took Inspiration from the findings of Hubel and Wiesel [1] who found that in the first processing layer (V1) of the visual cortex information is organized based on positions and orientations. As such, in my algorithms I analyze image data via densities on position-orientation space ℝ2×S1 that are obtained by filtering the image with filters that model the receptive fields of simple cells in V1 (Fig. 1A-C). In these new objects, the data lives on a non-Euclidean (curved) geometry of coupled positions and orientations. Via a sub-Riemannian geometry on the Lie group SE(2)≡ ℝ2⋊S1 one is able to model the perception of contours via sub-Riemannian geodesics [2,3], and generically deal with crossings as they are neatly disentangled in the higher dimensional representation (Fig.~1D-E).
Theoretical contributions
The academic focus of my past and present research lies within the overlapping fields of mathematics, computer science, and biomedical engineering. Throughout my thesis I employed a coherent mathematical (Lie) group theoretical approach to work on fundamental engineering problems in medical image analysis. The field of group theory studies a wide variety of mathematical entities using their symmetrical properties in a generic uniform manner. The thesis is primarily concerned with the processing and analysis of data that lives on the symmetry group SE(2) of planar rotations and translations. The group theoretical approach allows for algorithm design at a certain level of abstraction, allows us to work with simplified formulas (which would otherwise be intractable) and allows for natural extensions to other groups (e.g. from SE(2) to SO(3) as in [4] or SE(3) as in [5,6].
In the thesis I describe both practical results (fast, robust, and generic algorithms and significant clinical findings on systemic disease related vessel alterations), as well as new theoretical contributions such as:
- A new framework for computing data-adaptive sub-Riemannian geodesics in SE(2) [7,8,9,10,6].
- Object recognition via densities on SE(2) using a combination of smoothing splines, machine learning and hypo-elliptic smoothing priors [11,12,13,14].
Applications
The approach of image analysis via a sub-Riemannian geometry on SE(2) enabled the development of the following applications, each of which show state-of-the-art performance in extensive benchmark comparisons:
- Anatomical landmark detection via template matching, and template optimization in SE(2).
- Crossing preserving vessel enhancement via left-invariant processing of orientation scores.
- Vessel tracking and segmentation via local curve optimization.
- Vessel tracking via globally optimal sub-Riemannian geodesic extraction in SE(2), where we show clear benefits of our sub-Riemannian framework compared to the Riemannian counterparts in the image/orientation scores.
- Vessel geometry analysis and biomarker extraction by direct analysis of orientation scores.